一文搞懂 OTP 双因素认证

GitHub 在 2023 年 3 月推出了双因素认证（two-factor authentication）简称 2FA，并且承诺所有在 GitHub 上贡献的开发者在 2023 年底前启用双因素认证。因此最近在访问 GitHub 时如果注意的话经常会看到提示让在 2023 年 10 月 12 日之前开启，否则可能影响账户的使用：

如果之前没了解过这个概念，我们在开启之前不禁会想啥是双因素认证呢？如果你也有同样的疑问，那么耐心看完本文就能比较好的理解原理和使用了。so，让我们开始吧。

1.什么是双因素认证（2FA）

回想一下我们通常登录网站的时候通常输入用户名、密码就可以登录了，也就是说网站是通过用户名和密码来确认你的身份，假如其他人或者黑客通过一些手段获取到你的密码，那么他们就可以冒充你直接登录网站获取和你同等的服务，而网站对这一切并不知情，所以这个时候就需要借助于用户名和密码之外的其他方式来验证你的身份，这种例子也非常多。

例如我们首次登录支付宝、微信这类应用时需要填写手机验证码。早期在银行支付时需要使用银行下发给你的 U 盾或动态口令牌来确保只有你自己才可以支付，直到现在的指纹、刷脸支付其实都是在通过你持有的设备或你本身具有的生理特征来确保你就是你。

所以，所谓双因素认证（2FA）就是在用户名和密码认证之外再添加一种确认身份的方式，加强对账户的保护，至于具体的方式就有非常多了。包括我们上面说的最常用的短信验证码、指纹、刷脸，还有硬件方式的 U 盾、口令牌等，还有我们今天要说的 OTP （One-Time Password），也就是一次性密码的意思。上面这些方式都属于双因素认证，所以这个概念听起来很牛，其实是比较好理解的。

2.什么是 OTP

上面说了 OTP 全称 One-Time Password，也就是一次性密码，那么下面我们介绍下 OTP 的实现原理。

OTP 的实现主要有两种：

HOTP（HMAC-Based One-Time Password Algorithm）：基于 HMAC 的一次性密码。
TOTP（Time-Based One-Time Password Algorithm）：基于时间戳的一次性密码。

其中 HOTP 可以参考 RFC4226，TOTP 可以参考 RFC6238。

HOTP 出现的比较早，是基于 HMAC 实现的，其实 HMAC 就是 Hash + 消息或者说是 Hash + 盐（salt）来实现的，其中 Hash 函数通常采用 MD5、SHA 系列（SHA1/SHA256/SHA512 等）的单向消息摘要算法来实现。在 HOTP 中，Hash 函数采用 SHA1，在消息或者盐值部分放的是一个计数器，也就是一个大小为 8 字节的数字，主要的生成公式如下：

$$ HOTP = Truncate(HMAC_{SHA1}(key, counter)) $$

其中，key 表示对消息加密的密钥，counter 就是计数器的值。然后两者通过基于 SHA1 的 HMAC 算法计算出结果，所以结果长度是 20 字节，如果用 16 进制表示长度就是 40。由于结果太长了显然不利于用户输入，因此通过 Truncate 函数进行处理，处理成 6-8 位的数字，就和短信验证码一样，这样用户就可以很快的输入并进行验证。

上面只是计算 HOTP 结果主要的概括，至于具体的细节，例如 key 是如何编码的、counter 是怎么处理的以及至关重要的 Truncate 又是怎么工作的，这些下面会将，目前先不用关心，我们先有个整体的认识就可以了，如何计算并不影响具体的交互方式。

首先认证之前客户端和服务端都需要约定相同的 key 也就是密钥，而且这个密钥决不能泄露，否则也就是失去了 2FA 的意义，同时客户端和服务端也需要从相同的计数器值开始轮转，比如都从 1 开始，要增加一块增加，必须保证一致。也就是说 key 和 counter 必须都对起来，否则会验证失败，这个过程可以总结如下：

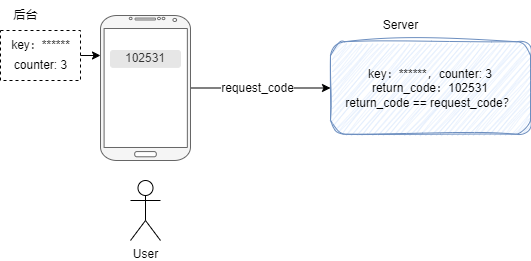
其实这个过程我们可以看出来一个比较明显的问题，就是计数器值需要保持一致。假如起始的计数器值是同步的，每次服务端需要用户输入的时候都自增一次，这个时候客户端打开生成 OTP 的客户端也自增一次，那么只要这个时候不小心刷新了浏览器或者触碰了手机的刷新，都会导致计数器不一致，从而动态密码失效。但是如果每次服务器都返回一个计数器值，用户还需要在手机端手动输入一次，操作起来比较麻烦。

那么这个时候我们会想，如何才能保证服务器和客户端没有任何交互就能拿到一个相同的计数器值呢？

可能我们这个时候很自然地会想到用时间，没错，时间就是一个天然的计数器，只要客户端和服务器能在时间上基本一致就可以，这个目前是比较容易保证的。事实上，TOTP 就是这么来的，它将计数器替换为时钟值，从而提供短暂的一次性密码，而且安全性也比较理想，所以目前被互联网广泛采用，TOTP 的算法和 HOTP 完全一样，只是将计数器换成了时间因子，其余的并没有变化，所以可以把 TOTP 看成 HOTP 的一个变体，上面的公式可以修改如下：

$$ TOTP = Truncate(HMAC_{SHA1}(key, T)) $$

其中 T 就是时间因子，注意我们这里说的是时间因子，可不可以直接用 Unix 时间戳呢？我们想一想，假如使用时间戳，单位是 s，就算服务端和客户端时间严格一致，那么我们输入一次性密码总归需要几秒的时间，这样一来受限于人的大脑和肢体反应速度，几乎是不可能登录成功的。所以如果只要能保证一次性密码在很小的一段时间内不变就可以，这个时间能比较充足的保证认证过程即可，在 TOTP 的 RFC 中是使用了步长（X）的概念，其默认值是 30s：

$$\begin{aligned} &X = 30 \\ &T = \frac{UnixTime}{X} \end{aligned}$$

这样相当于以 30s 为一个自然时间窗口，时间因子就表示当前是从 1970 年 1 月 1 日以来第几个 30s，所以在每一个窗口内，时间因子是固定不变的，这样就给用户留出充足的时间来输入一次性密码，同时对服务器和客户端的时间同步性要求也不会特别严格，时间差个几秒也不太会影响认证，最多也就是多输入一次，这样就比较好地解决了 HOTP 带来的计数器同步问题，所以结果换成了这样：

那么现在还有一个问题就是密钥（key）是怎么同步的，通常都是服务器生成一个唯一的密钥，客户端保存这个密钥，之后双方都是用这个密钥来生成一次性密钥。

首先在传输过程中肯定不能明文传输密钥，目前大部分网站都支持 HTTPS 访问，因此传输过程是安全的。其次就是在开启双因素认证时，必须是用户本人操作，假如被别人冒充，那么以后自己就再也无法登录自己的账户了，所以网站有个前提就是认为在开启双因素认证时，一定是用户本人操作的，为了提高安全性，也可以在开启一种认证方式是采用其他的方式进行认证，比如开启 HOTP 之前先验证手机或者邮箱，这样安全性会更高一些。

3.OTP 的计算过程

首先我们需要有一个密钥，这个是由服务器生成，密钥可以是一段随机生成的字节流，由于二进制不方便观察和输入，所以服务器会对这段二进制进行 base32 编码然后输出，当前主流的客户端都是支持以 base32 编码作为密钥输入的，我们下面用 Python 来生成一段随机密钥：

import os
import base64

# 由于 base32 需要 8 字节对齐，长度是原字符串的 8/5，为了不浪费空间密钥长度尽量是 5 的倍数
key = os.urandom(10)
encoded_key = base64.b32encode(key)
print(encoded_key)

这样我们就得到了一串密钥，假如编码后是：X2QEGOZX5PUBOQ52，然后将这段密钥给到客户端。

然后客户端要开始认证了，首先客户端要拿到时间因子，步长按照 30s 来算，可以按照下面的方式得到：

import time
# Python 3 整数相除 //
T = int(time.time()) // 30
print(T)

这样我们就得到了时间因子，假如当前是：56499675，然后我们根据上面的公式，我们需要来计算基于 SHA1 算法的 HMAC 结果，计算如下：

import struct
import base64
import hmac

key = base64.b32decode(encoded_key)
msg = struct.pack('>Q', T)
h = hmac.new(key, msg, digestmod='sha1')
value = h.digest()

密钥在进行计算时，仍然需要进行 base32 解码，然后使用原始的密钥参与计算，同时时间因子或者计数器的数字需要转换为原始的字节，按照要求是 8 个字节，按照大端（big-endian）的方式排列，所以我们使用 >Q 来编码，最后生成的 value 就是长度为 20 字节的摘要值。

然后我们要进行比较重要的一步 Truncate 操作，最终得到一次性密码，按照标准的定义实现如下：

取摘要结果最后的 4 位作为偏移（offset），范围一定在：0~15。
在摘要结果中从 offset 位置截取 4 个字节，去除符号位得到一个 31 位的整数，假设为 P。
设我们一次性密码的数字位数是：digit，我们只需要用上面的数字对 10 的 digit 次方取余便可得到一次性密码，也就是：P mod 10^digit

我们用代码表示如下：

offset = value[-1] & 0xf
P = (
    (value[offset] & 0x7f) << 24 
    | (value[offset+1] & 0xff) << 16 
    | (value[offset+2] & 0xff) << 8 
    | (value[offset+3] & 0xff)
)
digit = 6
code = P % 10**digit
# 408713
print(code)

这样我们就得到了 6 位数的验证码，当然上面的方法也有点小问题就是如果数字 P 比较小，那么结果可能不足 6 位，需要我们在前面补上 0，不过这不影响我们对算法本身的理解。

用户将得到的这个 code 输入之后，服务端会按照上面同样的过程进行计算，得到结果之后和客户端的输入进行比较，如果一致就验证通过了。

上面我们是用原生语言和标准库来实现的，事实上不需要这么麻烦，大多数编程语言都有自己的库，我们在开发时只需要调用库来计算就可以了，比如：

以 Python 的 pyotp 为例，首先需要简单安装一下：

pip3 install pyotp

然后就可以直接使用了，例如：

import pyotp

totp = pyotp.TOTP('X2QEGOZX5PUBOQ52')
code = totp.now()
print(code)
# 验证
assert totp.verify(code)

只需要简单两步就生成的一次性的密码，而且还直接提供了验证方法，非常方便。

4.使用场景案例

我们一般作为用户不需要自己写代码生成一次性密码，可以借助于各种第三方的 APP 帮助我们管理，常见的有 Google Authenticator、Microsoft Authenticator 等，我们以 GitHub 为例，看看是怎么开启的吧。

首先根据 GitHub 的提示我们点击 Enable 2FA，然后会跳转到新的页面：

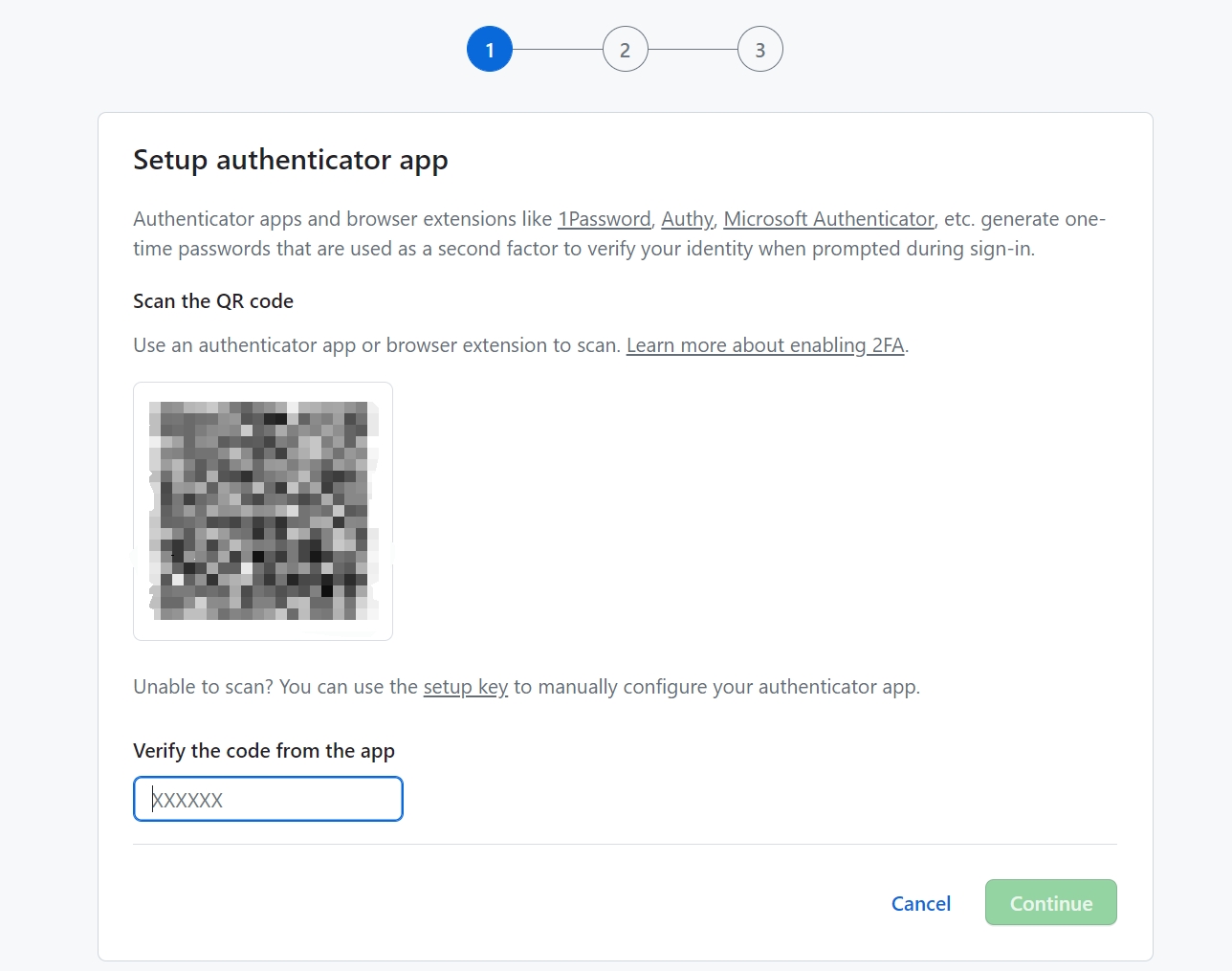
页面上提示我们可以使用 1Password、Authy、Microsoft Authenticator 等 APP 或者浏览器插件来生成一次性密码，通常使用手机 APP 更方便，这个时候我们以 Google Authenticator 为例来操作一下。

还是先安装 Google Authenticator，安装后打开，跳过登录 Google 账号这一步，点击右下角的加号会出现两个选项，分别是：扫描二维码、输入设置密钥。

由于应用做了限制不允许截图，所以这里先不放图了，当然操作也比较简单，我们直接选扫描二维码然后用手机扫描 GitHub 页面上这个二维码，就可以弹出一次性密码了，并且右侧会有倒计时表示当前一次性密码的过期时间，我们直接将密码填入输入框中，页面会跳到下一步。

这个时候 GitHub 会给我们一些恢复代码，防止因为手机丢失或者我们不小心误删了 APP 中的条目导致无法登录账户，这个时候需要将这些恢复代码保存好，以备不时之需。否则，万一手机出现故障那么就无法登录账户了。

当然我们也可以把上面二维码的内容保存下来，我们可以先解析出来上面的二维码，结果其实就是一段文本，例如：

otpauth://totp/GitHub:monchickey?secret=EPKCRBXZHDPHOOZH&issuer=GitHub

前面的 otpauth 表示协议，totp 表示采用基于时间的一次性密码，GitHub 说明发行者是 GitHub，后面的格式就是：<用户名>?secret=<密钥 base32 值>&issuer=<发行者>。

Note: 顺便说一下尽量不要用微信、浏览器或其他在线工具解析二维码，个人感觉是存在风险的，最好用离线的工具或者干脆自己用代码解析一下都可以，比如可以用 CairoSVG 将 SVG 图片转换为 PNG，然后使用 ZBar 解析内容。

了解了这段文本的含义，我们就可以提前将上面这段文本安全地保存到其他地方，之后就算手机出现问题，我们也可以重新在 APP 中选择以密钥添加，仍然可以正常生成一次性密码。所以为了安全起见，所有涉及到双因素认证的一次性密码场景，我们有条件最好都保存下密钥，前提密钥要保存到安全的地方。

拓展一下如果我们作为服务端的开发者，也可以直接生成上面格式的文本，还是以 pyotp 为例：

import os
import base64
import pyotp

key = os.urandom(10)
encoded_key = base64.b32encode(key)

totp = pyotp.TOTP(encoded_key)
auth_text = totp.provisioning_uri(name='alice', issuer_name='Orange')

然后我们将生成的认证文本转换成二维码输出就可以了。

最后一步，我们就成功地开启了 GitHub 的 2FA：

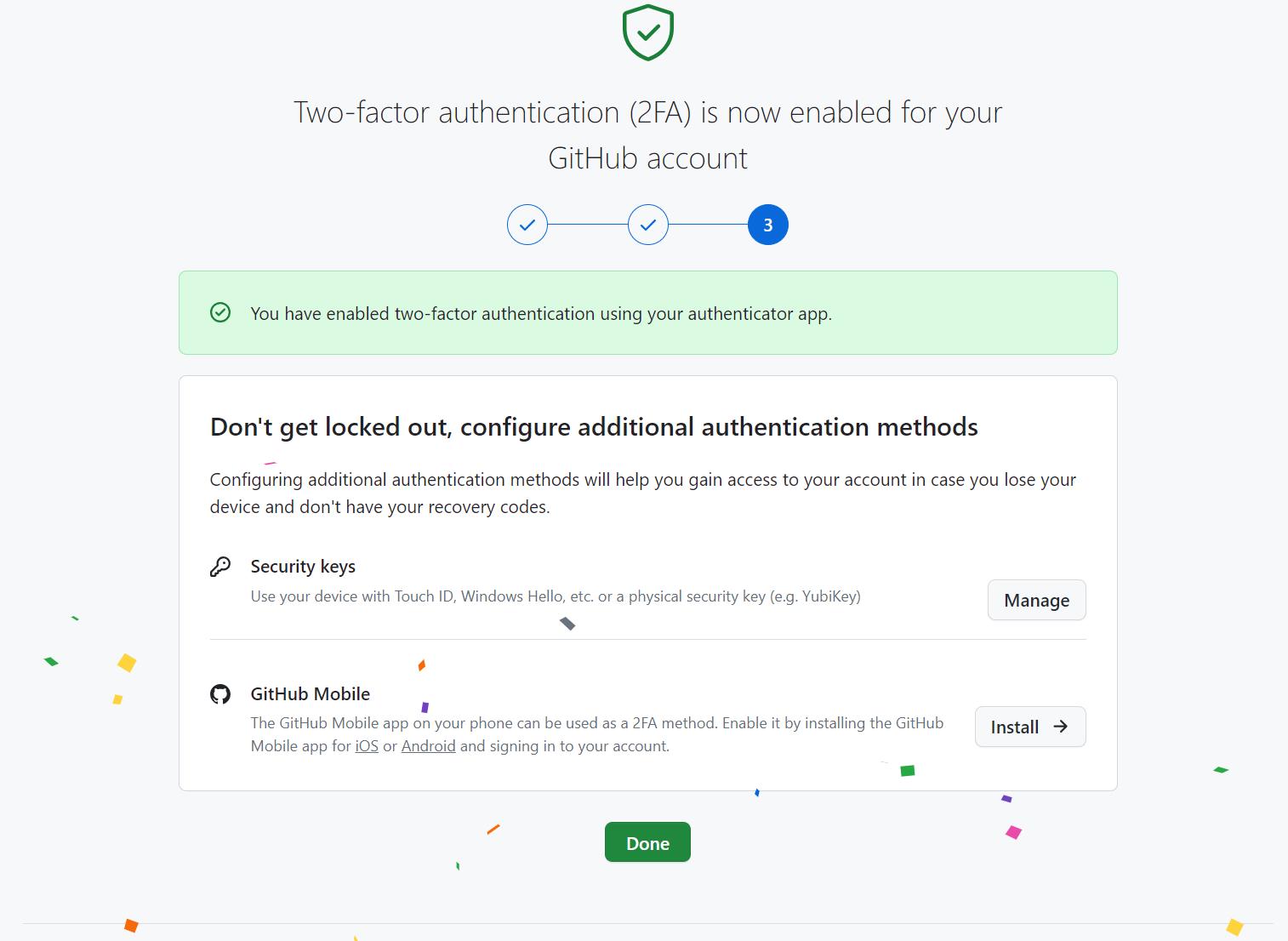
相信到这里，我们都应该理解 2FA 和 OTP 的概念和原理了，如果你的 GitHub 还没有开启，就赶快操作开启吧~

Reference:

monchickey

2023/09/18

1.什么是双因素认证（2FA）

2.什么是 OTP

3.OTP 的计算过程

4.使用场景案例